Markov chains & transition probability matrix

Markov chains

In machine learning algorithms, Markov chains are widely applied in time series models. The main idea is that regardless of the initial state, as long as the state transition matrix remains unchanged, the final state will always converge to a fixed value. This memory-lessness is called the Markov property. The equation is as below:
$$
P(x_{t+1}∣…,x_{t−2},x_{t−1},x_{t})=P(x_{t+1}∣x_{t})\tag{1}
$$

Transition probability matrix

Each element of the matrix is represented by a probability. The values are non-negative, and the sum of the elements in each row equals 1. Under certain conditions, they can transition between each other, hence it is called a transition probability matrix. The two-step transition probability matrix is exactly the square of the one-step transition probability matrix. The $𝑘$ step transition probability matrix is the $𝑘^{th}$ power of the one-step transition probability matrix. In the $𝑘$ step transition probability matrix, the sum of the elements in each row is also 1.

Implementation

For example, the value of $P(i,j)$ in matrix is $P(j|i)$, which is the probability of from state $i$ to state $j$. The transition probability matrix is as below：
$$
\begin{bmatrix} 0.9 & 0.075 & 0.025 \\ 0.15 & 0.8 & 0.05 \\ 0.25 & 0.25 & 0.5 \end{bmatrix}\tag{2}
$$

Exercise

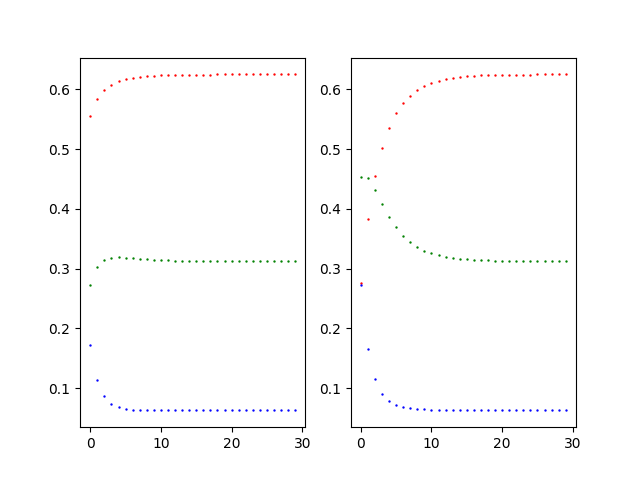
Giving an initial state $P_{01}=[0.5,0.2,0.3]$ and $P_{02}=[0.1,0.4,0.5]$, the 𝑘 step transition is $P_0=P_0∗P_k$. $P_0$ can reach a stable value after multiple iterations. If k=30, please calculate the eventual result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import pylab as pl

p01 = np.array([0.5, 0.2, 0.3]) 
p02 = np.array([0.1,0.4,0.5]) 
p = np.array([[0.9, 0.075, 0.025], [0.15, 0.8, 0.05],[0.25, 0.25, 0.5]])
n = 30
c = np.array(['r','g','b'])       
def calanddraw(p0,p ):
  for i in range(n):
     p0 = np.mat(p0) * np.mat(p)       
     for j in range(len(np.array(p0)[0])):
          pl.scatter(i,p0[0,j], c = c[j], s=.5)
pl.subplot(121)
calanddraw(p01,p)
pl.subplot(122)
calanddraw(p02,p)
pl.show()

From the figure below we can reach the conclusion that both states converge eventually and their value are close to each other.

image.png

Model-based algorithms

Value iteration

Unlike simply times initial state with transition probability matrix multiple times, value iteration is a commonly used dynamic planning (DP) method (DP methods assume that we have a perfect model of the environment’s MDP. That’s usually not the case in practice, but it’s important to study DP anyway), which is mainly used to solve the optimal strategy problem in Markov Decision Process (MDP). The core idea of the Value Iteration algorithm is to update the value function of the state iteratively, gradually approaching the optimal value function, so as to obtain the optimal policy. The main advantage of the value iteration algorithm is that it is simple and easy to implement, and it is applicable to various types of MDP problems. However, the main disadvantage of the value iteration algorithm is its high time complexity, especially when the state space is large. Therefore, in practical applications, the value iteration algorithm usually needs to be combined with other optimization techniques, such as dynamic programming optimization and parallel computing, to improve the computational efficiency. The equation of algorithm is as below.

Overview

$$
V_{(k+1)}(s)=max_a[R(s,a)+γ_{Σs^′∈S}P(s^′|s,a)V^k(s^′)]\tag{3}
$$

First, we start with a random value function $V(s)$. At each step, we update it. Hence, we look ahead one step and go over all possible actions at each iteration to find the maximum. Moreover, the only difference is that in the value iteration algorithm, we take the maximum number of possible actions. Instead of evaluating and then improving, the value iteration algorithm updates the state value function in a single step. In particular, this is possible by calculating all possible rewards by looking ahead. Finally, the value iteration algorithm is guaranteed to converge to the optimal values.

Implementation

This is the entire code of value iteration implementation. I will break down every line and explain.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np

def value_iteration(states, actions, transition_prob, reward, discount_factor=0.9, theta=1e-6):

    value_function = np.zeros(len(states))

    policy = np.zeros(len(states), dtype=int)

    while True:
        delta = 0
        for s in states:
            v = value_function[s]
            action_values = np.zeros(len(actions))
            for a in actions:
                action_value = 0
                for next_s in states:
                    prob = transition_prob.get((s, a, next_s), 0)
                    action_value += prob * (reward.get((s, a, next_s), 0) + discount_factor * value_function[next_s])
                action_values[a] = action_value
            value_function[s] = max(action_values)
            delta = max(delta, abs(v - value_function[s]))

        if delta < theta:
            break

    for s in states:
        action_values = np.zeros(len(actions))
        for a in actions:
            action_value = 0
            for next_s in states:
                prob = transition_prob.get((s, a, next_s), 0)
                action_value += prob * (reward.get((s, a, next_s), 0) + discount_factor * value_function[next_s])

            action_values[a] = action_value
        policy[s] = np.argmax(action_values)

    return policy, value_function


states = [0, 1, 2]
actions = [0, 1]
transition_prob = {
    (0, 0, 0): 0.5, (0, 0, 1): 0.5,
    (0, 1, 0): 0.2, (0, 1, 1): 0.8,
    (1, 0, 0): 0.7, (1, 0, 2): 0.3,
    (1, 1, 1): 0.6, (1, 1, 2): 0.4,
    (2, 0, 2): 1.0,
    (2, 1, 1): 0.5, (2, 1, 2): 0.5,
}
reward = {
    (0, 0, 0): 1, (0, 0, 1): 1,
    (0, 1, 0): 0, (0, 1, 1): 1,
    (1, 0, 0): 1, (1, 0, 2): 2,
    (1, 1, 1): 0, (1, 1, 2): 3,
    (2, 0, 2): 0,
    (2, 1, 1): 1, (2, 1, 2): 0,
}

policy, value_function = value_iteration(states, actions, transition_prob, reward)
print("Optimal Policy:", policy)
print("Value Function:", value_function)

It will be much easier to understand the algorithm with a practice. So we can try to explain value iteration well by a simple implementation. We first import NumPy, of course. Then definite a function, which is the main character of this section: value iteration. This function requires several input values including states, actions, transition probability, reward, discount factor and theta. In this implementation, $γ=0.9$,$$θ=1^{−6}$$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

defvalue_iteration(states, actions, transition_prob, reward, discount_factor=0.9, theta=1e-6):
"""
    Performs value iteration for a given MDP.

    :param states: List of states
    :param actions: List of actions
    :param transition_prob: A dictionary that maps (state, action, next_state) to the transition probability
    :param reward: A dictionary that maps (state, action, next_state) to a reward
    :param discount_factor: Discount factor (gamma)
    :param theta: A threshold for convergence
    :return: A tuple (policy, value_function)
    """

In this function, we need to create two arrays for the storage of possible state and policy. State is easy to understand, but what is “policy”?

A policy is a strategy that an agent uses in pursuit of goals. The policy dictates the actions that the agent takes as a function of the agent’s state and the environment. In reinforcement learning, a policy is a strategy used by an agent to determine its actions at any given state. Formally, a policy is a mapping from states of the environment to actions to be taken when in those states. It can be deterministic or stochastic.

Deterministic Policy: This type of policy maps each state to a specific action. If π is a deterministic policy and s is a state, then π(s) is the action taken when in state s.

Stochastic Policy: This type of policy provides a probability distribution over actions for each state. If π is a stochastic policy and s is a state, then π(a|s) represents the probability of taking action a when in state s.

1
2
value_function = np.zeros(len(states))
   policy = np.zeros(len(states), dtype=int)

Then we enter the iteration of value function. Before start iteration, we have to define a variable called Δ. It is a variable used to record the variation of value function in a iteration and can judge whether the iteration is converging. for s in states is a order asking agent to go through every state, v = value_function[s] is to store all the result of s in v. These are the pre-moves of iteration.

1
2
3
4
5
while True:
    delta = 0
    for s in states:
        v = value_function[s]
        action_values = np.zeros(len(actions))

The result of value function comes from the maximum value of action values. We create an empty array for the storage of action values. Firstly initialize action value, then for each action, we go through every possible next state. After cumulating action value based on bellman function and store them as an array, we can obtain the maximum action value and take it as the value function value of current state.

In order to judge the convergency, update delta (Δ) at the end of value function calculation. abs(v - value_function[s]) is the variation of value function. We determine the value of delta by comparing the value between previous Δ and new Δ and taking the maximum value. Cycle will ceased if the update range smaller than θ.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
action_values = np.zeros(len(actions))
   for a in actions:
        # go through every possible action
               action_value = 0
           # initialize action value
               for next_s in states:
               # go through every possible next state
                   prob = transition_prob.get((s, a, next_s), 0)
               # achieve transition probability (0 if not exist)
                   action_value += prob * (reward.get((s, a, next_s), 0) + discount_factor * value_function[next_s])
               # cumulative action value based on bellman function
               action_values[a] = action_value
               # store result in array of action value
           value_function[s] = max(action_values)
           # update value fuction and obtain maximum value among all the possible action value
           delta = max(delta, abs(v - value_function[s]))
           # update delta and record maximum variation

       if delta < theta:
           break

Simultaneously, we try to find the optimal policy. Basically trying to find the action which can bring maximum action value in each state then form a sequence by combining these actions.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
for s in states:
   # go through every state
       action_values = np.zeros(len(actions))
       # initialize array
       for a in actions:
       # go through every possible action
           action_value = 0
           # initialize current action value
           for next_s in states:
               prob = transition_prob.get((s, a, next_s), 0)
               action_value += prob * (reward.get((s, a, next_s), 0) + discount_factor * value_function[next_s])
               # obtain current state, reward of taking action to next state & calculate discounted future value
           action_values[a] = action_value
       policy[s] = np.argmax(action_values)
       # return optimal policy

   return policy, value_function

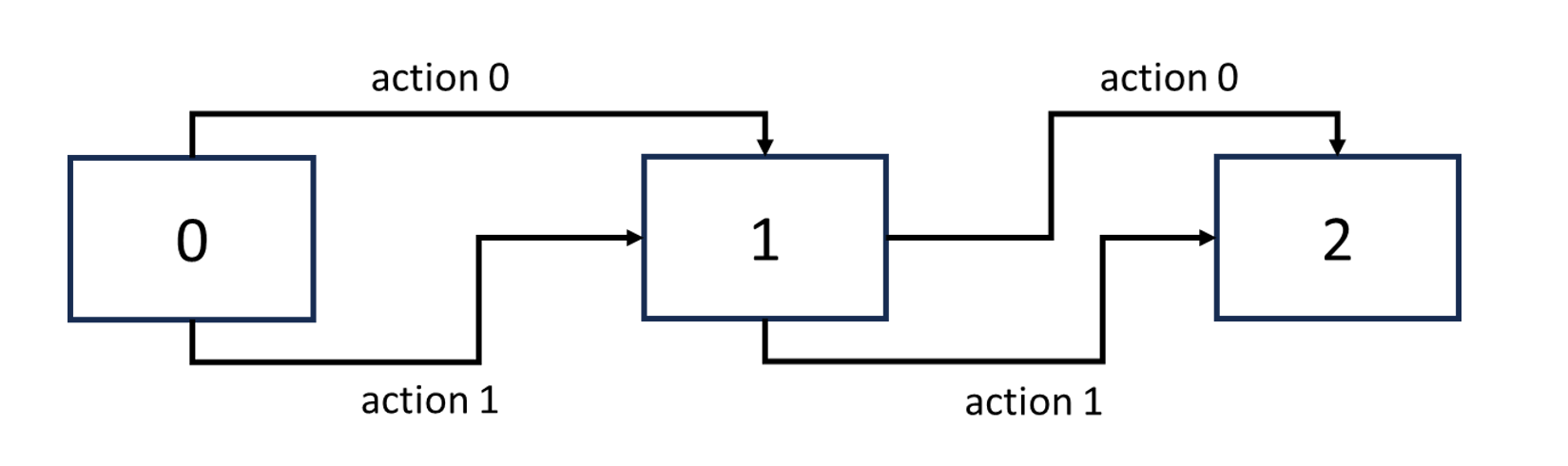
Here is the exercise. In this virtual environment, we can observe three states: 0, 1, 2 and two actions: 0 and 1. The corresponding transition probability and reward table is as below. In this exercise, transition probability means the state have the probability of remaining at the same state. For example, if we are at state 0 and take action 0, we have 50% probability stay at the same state. In addition, (1, 0, 0): 0.7 means if we at state 1 and take action 0, we can have 70% probability return to state 0 ; (2, 1, 1): 0.5 means if we at state 2 and take action 1, we can have 50% probability return to state 1.

scenario state action next state transition probability reward
a11 0 0 0 0.5 1
a12 0 0 1 0.5 1
a21 0 1 0 0.2 0
a22 0 1 1 0.8 1
b11 1 0 0 0.7 1
b12 1 0 2 0.3 2
b21 1 1 1 0.6 0
b22 1 1 2 0.4 3
c11 2 0 2 1.0 0
c21 2 1 1 0.5 1
c22 2 1 2 0.5 0.5

image.png

Diagram of state, action and transition

Since we have complete all the requisite, we can run the code and get the result.

Optimal Policy: 0→0→1

Value Function: [10.16927311, 10.20689125, 9.26018305]

Policy iteration

The other common way that MDPs are solved is using policy iteration – an approach that is similar to value iteration. While value iteration iterates over value functions, policy iteration iterates over policies themselves, creating a strictly improved policy in each iteration (except if the iterated policy is already optimal).

Policy iteration first starts with some (non-optimal) policy, such as a random policy, and then calculates the value of each state of the MDP given that policy — this step is called policy evaluation. It then updates the policy itself for every state by calculating the expected reward of each action applicable from that state.

The basic idea here is that policy evaluation is easier to computer than value iteration because the set of actions to consider is fixed by the policy that we have so far.

Policy evaluation

policy evaluation is an evaluation of the expected reward of a policy. Vπ(s), the expected reward of policy π from state s, is the weighted average of reward of the possible state sequences defined by that policy times their probability given π. Policy evaluation can be defined by the following equation:
$$
V^π(s)=∑P_{π(s)}(s^′|s)[r(s,a,s^′)+γV^π(s^′)]\tag{4}
$$
Where $V^π(s)=0$ is for terminal state. Note that this is very similar to the Bellman equation, except $V^π(s)$ is not the value of the best action, but instead just as the value for $π(s)$, the action that would be chosen in s by the policy $π$. Note the expression $P_{π(s)}(s^′∣s)$ instead of $P_a(s^′∣s)$, which means we only evaluate the action that the policy defines.

Policy improvement

If we have a policy and we want to improve it, we can use policy improvement to change the policy (that is, change the actions recommended for states) by updating the actions it recommends based on $V(s)$ that we receive from the policy evaluation.

Let Qπ(s,a) be the expected reward from s when doing a first and then following the policy π. Recall from the chapter on Markov Decision Processes that we define define this as:
$$
Q_π(s,a)=∑P_a(s^′|s)[r(s,a,s^′)+γV^π(s^′)\tag{5}
$$
If there is an action a make $Q_π(s,a)>Q_π(s,π(s))$, then the policy π can be strictly improved by setting $π(s)←a$. This will improve the overall policy.

Implementation

In this implementation, we have two states and 2 actions. reward during iteration can be 0 or 1. Discount factor $γ=0.9$.

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import copy

states = ['1', '2']
actions = ['a', 'b']
rewards = [0, 1]
discount_factor = 0.9

q_value = {states[0]: {actions[0]: 0, actions[1]: 0}, states[1]: {actions[0]: 0, actions[1]: 0}} 

pi = {states[0]: {actions[0]: 0.5, actions[1]: 0.5}, states[1]: {actions[0]: 0.5, actions[1]: 0.5}}

Code shown below is the transition probability and reward. We can visually obtain information through table below.

Scenario next state transition probability reward
1a1 1 1/3 0
1a2 2 2/3 1
1b1 1 2/3 0
1b2 2 1/3 1
2a1 1 1/3 0
2a2 2 2/3 1
2b1 1 2/3 0
2b2 2 1/3 1

It will be more clearer when explaining the meaning through one of the scenarios. For example, we are at state 1, if we take action $a$ , we have a $\frac{2}{3}$ probability of reaching the next state and receive reward = 0 or $\frac 1 3$ probability of staying at the same state and receive reward = 1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def p_s_r(state, action):
    if state == "1":
        if action == "a":
            return ((1.0 / 3, "1", 0),
                    (2.0 / 3, "2", 1))
        else:
            return ((2.0 / 3, "1", 0),
                    (1.0 / 3, "2", 1))
    if state == "2":
        if action == "a":
            return ((1.0 / 3, "1", 0),
                    (2.0 / 3, "2", 1))
        else:
            return ((2.0 / 3, "1", 0),
                    (1.0 / 3, "2", 1))

Next part is state evaluation function. In this function, we initialize the function and define the value of θ. deepcopy means to copy current V value to old V value for judgement of convergence. Then, assemble to value iteration, we go through every possible action in every state and obtain corresponding transition probability and reward. After that, we calculate Q value (action value) and V value. If the variation of V value smaller than θ, we can conclude that the function is converged and break the cycle.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def policy_evaluate():
    v_value = {states[0]: 0, states[1]: 0}
    threshold = 0.0001
    while True:
        v_value_old = copy.deepcopy(v_value)

        for s in states:
            temp_v = 0
# temp_q = 0
            for a, p in pi[s].items():
                temp_q = 0
                for t in p_s_r(s, a):
                    p_s_s1, s_, r = t[0], t[1], t[2]
                    temp_q += p_s_s1 * (r + discount_factor * v_value[s_])
                q_value[s][a] = temp_q
                temp_v += p * temp_q
            v_value[s] = temp_v


        delta = 0
        for i in range(len(v_value)):
             delta += np.abs(v_value[states[i]] - v_value_old[states[i]])
        if delta <= threshold:
        	break

	return v_value

Next, we update policy based on the V value we got. Before we enter the cycle, we have to clarify what is done = True . done = True means cease the operation when the policy becomes stable.

The function, policy_improve is used to find out the optimal action in current state and turn its probability of been selected to 1. Meanwhile, the probability of choosing other actions will be 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def policy_improve(v):
    done = True

    for s in states:
        action = max(q_value[s],key=q_value[s].get)
    # print(action)
        for k in pi[s]:
            if k == action:
                if pi[s][k] != 1.0:
                    pi[s][k] = 1.0
                    done = False
            else:
                pi[s][k] = 0.0
    return done

The iteration in this implementation is quite simple - only 2 times. Activate the code we can get the results shown as below:

State 1 2
V value 6.666339540673712 6.666353680224912
Q value State 1 State 2
action a 6.666339540673712 6.666353680224912
action b 6.333001354313227 6.333029633415626
State 1 2
Policy a = 1, b = 0 a = 1, b = 0 
1
2
3
4
5
6
7
8
9
10
11
12
if __name__ =='__main__':
    is_done =False
    i =0
while is_doneisFalse:
        v = policy_evaluate()
        is_done = policy_improve(v)
        i +=1

print('Policy-Iteration converged at step %d.' % i)
print(v)
print(q_value)
print(pi)

Difference between value iteration and policy iteration

Aspect Value iteration Policy iteration
Methodology Iteratively updates value functions until convergence Alternates between policy evaluation and improvement
Goal Converges to optimal value function Converges to the optimal policy
Execution Directly computes value functions Evaluate and improve policies sequentially
Complexity Typically simpler to implement and understand Involves more steps and computations
Convergence May converge faster in some scenarios Generally converges slower but yields better policies

In summary, both value iteration and policy iteration are effective methods for solving RL problems and deriving optimal policies. Value iteration directly computes optimal value functions iteratively, which can converge faster in some cases and is generally simpler to implement. On the other hand, policy iteration alternates between evaluating and improving policies, resulting in slower convergence but potentially yielding better policies overall. Understanding the differences between these approaches is crucial for selecting the most suitable algorithm based on the problem requirements and computational constraints.