Model-based / Model-free RL

Everybody knows reinforcement learning is one of a machine learning methods aiming to make agent explore and find the optimal policy through interactions with environment and maximize cumulative reward. Before starting this passage, we have to understand what is model-free and what is model-based?

image.png

Monte-Carlo (MC)

Overview

The Monte Carlo algorithm is a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The core idea is to use randomness to solve problems that might be deterministic in principle. The key concepts of MC are: random sampling, estimation by taking the average of outcomes from random samples, applicability of high-dimensional spaces. It can be used in simulations, optimization, numerical integration, financial anticipation and statistical physics. Advantages and disadvantages of MC are shown in the table below.

Monte Carlo Advantages Disadvantages
1 Simple to implement Can be computationally intensive
2 Flexible and can handle a wide range of problems Convergence can be slow
3 Suitable for high-dimensional integrals Results are probabilistic, not deterministic

Here is a classic example of MC application: Estimate the value of $π$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import random

defestimate_pi(num_samples):
    inside_circle =0

for _inrange(num_samples):
        x = random.uniform(0,1)
        y = random.uniform(0,1)

if x**2 + y**2 <=1:
            inside_circle +=1

return (inside_circle / num_samples) *4

pi_estimate = estimate_pi(100000)
print(f"Estimated value of π:{pi_estimate}")

The result is π: 3.13544.

Assuming we have a state sequence under a policy π:
$$
[S_1,A_1,R_1,S_2,A_2,R_2,S_3,A_3,R_3,…,S_T,A_T,R_T]\tag{1}
$$
In MDP, the value function is:
$$
v_π(s)=E_π[G_t|S_t=s]G_t=R_{t+1}+γR_{t+2}+…+γ^{T−t−1}R_Tv_π(s)≈average(G_t)\tag{2}
$$
However, the average consumes so many storage. A better method is obtaining average value in iterations:
$$
μt=\frac 1 t ∑j=\frac 1 t x_j=\frac 1 t (x_t+\sum_{j=1}^{t−1}x_j)=μ_{t−1}+\frac 1 t (x_t−μ_{t−1})\tag{3}
$$

Q Learning: the first step of model-free RL

Algorithm

Q learning is a value-based RL algorithm. Thus, Q value is the fundamental variable in this algorithm, and this is the reason why this algorithm called “Q Learning”. Assuming we already know what is agent, what is environment, what are the states, the actions have to be discrete and the reward function, let us cut to the point and introduce the learning method of agent in Q Learning.
$$
Q(s,a)\leftarrow Q(s,a)+α(r+γmax_{a^′}Q(s^′,a^′)−Q(s,a))\tag{4}
$$
Equation above is the update method of Q value. α is learning rate (basically learning rate defines the pace of updating), γ is discount factor. $Q(s,a)$ is the action value of current state; $Q(s^′,a^′)$ is the action value of next state; $max_{a^′}Q(s^′,a^′)$ means choosing the maximum $Q(s^′,a^′)$ among all the possible actions.

The Q learning is quite similar to value iteration. We are going to explain the differences between Q learning and value iteration in detail through a simple implementation.

Implementation

Environment

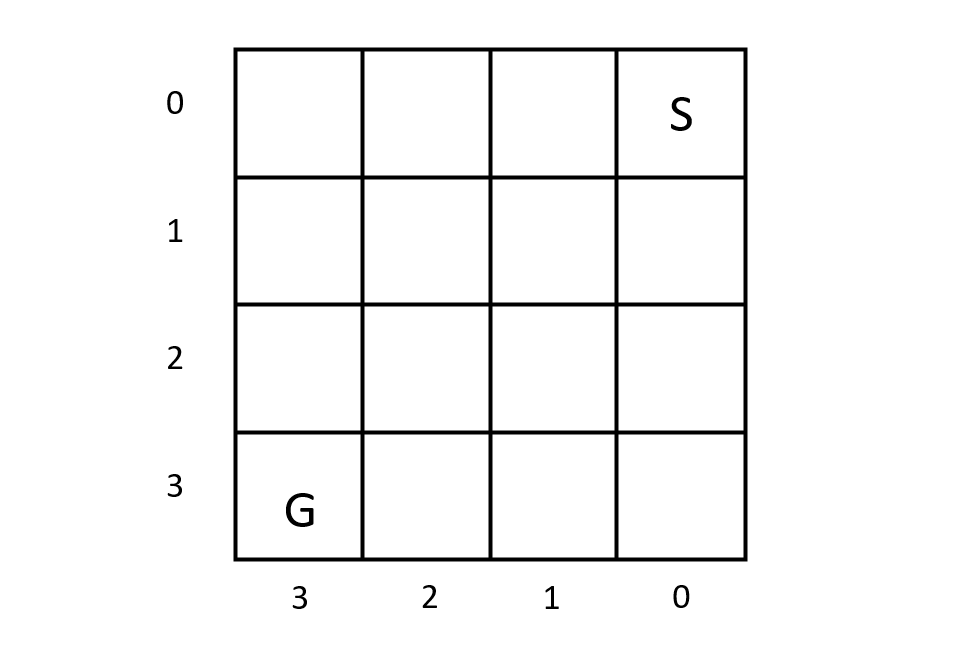
The environment is a 4x4 grid. Our target is to train the agent and let it successfully moves from (0, 0) to (3,3).

image.png

1
2
3
grid_size = 4
goal_state = (3,3)
start_state = (0,0)

Hyperparameters

$ϵ$ means the agent have probability equals to ϵ choosing a random action and $(1-ϵ)$ probability choosing the optimal action.

1
2
3
4
alpha =0.1 #learning rate
gamma =0.9 #discount factor
epsilon =0.1 #epsilon-greedy
num_episodes = 1000

State(s) and action(s)

The state is just all the points in the 4x4 girds. We create two functions for action selection and transition to next state.

In function get_next_state, the current coordinates based on the action:

  • If the action is 'up' and x is greater than 0, it moves up by decrementing x by 1.
  • If the action is 'down' and x is less than grid_size - 1, it moves down by incrementing x by 1.
  • If the action is 'left' and y is greater than 0, it moves left by decrementing y by 1.
  • If the action is 'right' and y is less than grid_size - 1, it moves right by incrementing y by 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def get_next_state(state, action):
    x, y = state
    if action == 'up' and x > 0:
        x -= 1
    elif action == 'down' and x < grid_size - 1:
        x += 1
    elif action == 'left' and y > 0:
        y -= 1
    elif action == 'right' and y < grid_size - 1:
        y += 1
    return (x, y)

actions = ['up','down','left','right']
num_actions =len(actions)

def choose_action(state):
	if np.random.uniform(0,1) < epsilon:
		return np.random.choice(num_actions)
	else:
		return np.argmax(Q_table[state[0], state[1], :])

Reward function

Agent will get reward = 100 if arriving at (3, 3), otherwise -1.

1
2
3
4
5
def get_reward(state):
	if state == goal_state:
		return 100
	else:
		return -1

Q value function

This part is the fundamental training loop of algorithm. while state != goal_state means continues iterations until the goal state is reached; action_index = choose_action(state) means select an action index based on policy which not shown; action = actions[action_index]is to convert the action index to an actual action; next_state = get_next_state(state, action) is used to determine the next state based on the current state and action; finally,reward = get_reward(next_state)can calculate the reward for transitioning to the next state.

Then, we store Q value under current (s, a) pair in Q table, computes the maximum Q value for next state and updates Q value for current $(s,a)$ pair using Q learning update rule.

Since we have the maximum Q value of each state stored in Q table, we can try to compute the optimal policy and turn it into the form of path.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
for episodeinrange(num_episodes):
    state = start_state
while state != goal_state:
        action_index = choose_action(state)
        action = actions[action_index]
        next_state = get_next_state(state, action)
        reward = get_reward(next_state)

        Q_table[state[0], state[1], action_index] += alpha * (
                reward + gamma * np.max(Q_table[next_state[0], next_state[1], :]) - Q_table[
            state[0], state[1], action_index]
        )

        state = next_state

print("Final Q-Table:")
print(Q_table)

state = start_state
path = [state]
while state != goal_state:
    action_index = np.argmax(Q_table[state[0], state[1], :])
    action = actions[action_index]
    state = get_next_state(state, action)
    path.append(state)

print("Path from start to goal:")
print(path)

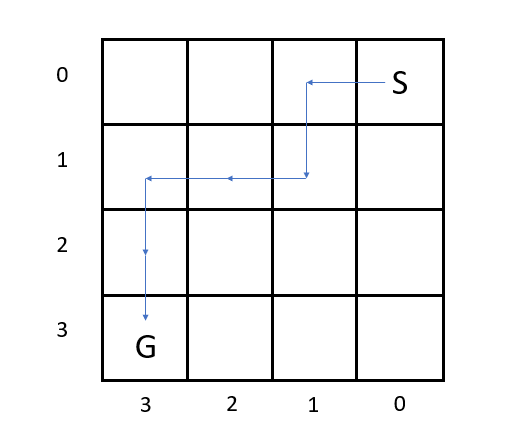
Results

The path after training is shown in the figure.

image.png

Sarsa: An on-policy RL algorithm

Difference between on-policy & off-policy

In reinforcement learning, two different policies are also used for active agents: a behavior policy and a target policy. A behavior policy is used to decide actions in a given state (what behavior the agent is currently using to interact with its environment), while a target policy is used to learn about desired actions and what rewards are received (the ideal policy the agent seeks to use to interact with its environment).

If an algorithm’s behavior policy matches its target policy, this means it is an on-policy algorithm. If these policies in an algorithm don’t match, then it is an off-policy algorithm.

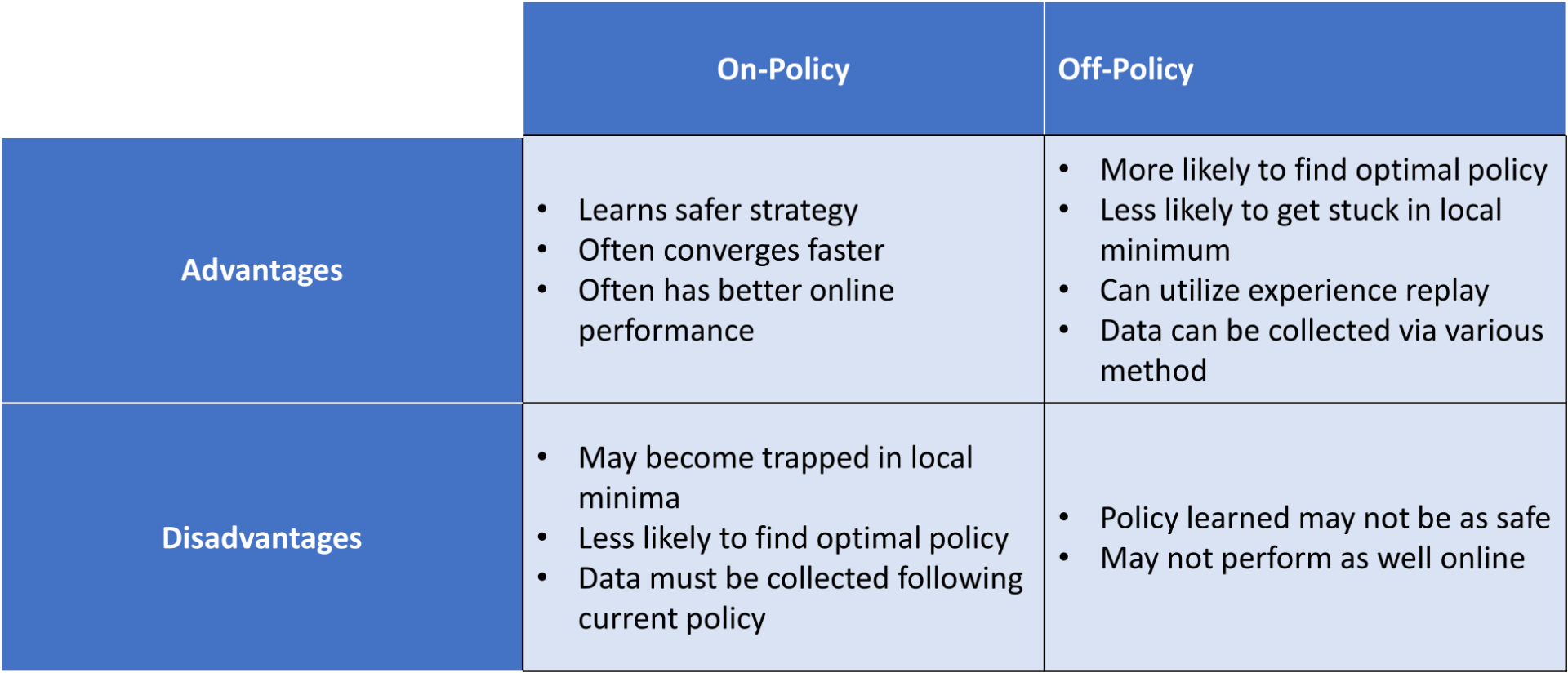
image.png

Sarsa operates by choosing an action following the current epsilon-greedy policy and updates its Q values accordingly. On-policy algorithms like Sarsa select random actions where non-greedy actions have some probability of being selected, providing a balance between exploitation and exploration techniques. Since Sarsa Q values are generally learned using the same epsilon-greedy policy for behavior and target, it classifies as on-policy.

Q learning, unlike Sarsa, tends to choose the greedy action in sequence. A greedy action is one that gives the maximum Q value for the state, that is, it follows an optimal policy. Off-policy algorithms like Q learning learn a target policy regardless of what actions are selected from exploration. Since Q learning uses greedy actions, and can evaluate one behavior policy while following a separate target policy, it classifies as off-policy.

Algorithm

SARSA, unlike Q learning, is an on-policy algorithm, which means it updates the policy based on the actions taken. Quite like policy iteration. But in Sarsa, the update of policy will not be as “hard” as policy iteration since we have the influence of learning rate $α$.

Still, the algorithm keeps updating Q value. One thing different is agent of Sarsa already come up with which action to choose and predict next state and next action. That is why the algorithm called SARSA - State, Action, Reward, State, Action.

Implementation

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np

# Maze
maze = np.array([
    [0,0,0,0],
    [0, -1,0, -1],
    [0,0,0, -1],
    [-1,0,0,1]
])

# Start state and terminal state
start_state = (3,0)
goal_state = (3,3)

# action space
actions = [(0,1), (0, -1), (-1,0), (1,0)]

# initialize value function
Q = np.zeros((4,4,4))

# hyperparameters
alpha = 0.1
gamma = 0.9
epsilon = 0.1
max_episodes = 100

# SARSA
for episodeinrange(max_episodes):
    state = start_state
    action = np.random.choice(range(4))if np.random.rand() < epsilonelse np.argmax(Q[state])

while state != goal_state:
# next_state = (state[0] + actions[action][0], state[1] + actions[action][1])
        a = state[0] + actions[action][0]
        b = state[1] + actions[action][1]
if a >3:
            a-=1
elif b >3:
            b-=1
elif a < -4:
            a+=1
elif b < -4:
            b+=1
        next_state = (a,b)
        reward = maze[next_state]
        next_action = np.random.choice(range(4))if np.random.rand() < epsilonelse np.argmax(Q[next_state])
        Q[state][action] += alpha * (reward + gamma * Q[next_state][next_action] - Q[state][action])

        state = next_state
        action = next_action

# print result
for iinrange(4):
for jinrange(4):
print("State:", (i, j))
print("Up:", Q[i][j][0])
print("Down:", Q[i][j][1])
print("Left:", Q[i][j][2])
print("Right:", Q[i][j][3])
print()

Result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
State: (0, 0)
Up: -0.008042294056935573
Down: -0.007868742418369764
Left: -0.016173595452674966
Right: 0.006662566560762523

State: (0, 1)
Up: 0.048576025675988774
Down: -0.0035842473161881465
Left: 0.024420015715567546
Right: -0.46168987981312615

State: (0, 2)
Up: 0.04523751845081987
Down: 0.04266319340558091
Left: 0.044949583791193154
Right: 0.026234839551098416

State: (0, 3)
Up: 0.01629652821649763
Down: 0.050272192325180515
Left: -0.009916869922464355
Right: -0.4681667868865369

State: (1, 0)
Up: -0.09991342319696966
Down: 0.0
Left: 0.0
Right: 0.036699099068340166

State: (1, 1)
Up: 0.008563965102313987
Down: 0.0
Left: 0.0
Right: 0.3883250678150607

State: (1, 2)
Up: -0.3435187267522706
Down: -0.2554776873673874
Left: 0.05651543121932354
Right: 0.004593450910446022

State: (1, 3)
Up: -0.1
Down: -0.013616634831997914
Left: 0.01298827764814053
Right: 0.0

State: (2, 0)
Up: 0.28092113053540924
Down: 0.0
Left: 0.0024286388798406364
Right: 0.06302299434701504

State: (2, 1)
Up: 0.0
Down: 0.0
Left: -0.16509175606504775
Right: 1.9146361697676122

State: (2, 2)
Up: -0.1
Down: 0.0
Left: 0.03399106390140035
Right: 0.0

State: (2, 3)
Up: -0.3438668479533914
Down: 0.004696957810272524
Left: -0.19
Right: 0.0

State: (3, 0)
Up: 3.3060693607932445
Down: 0.8893977121867367
Left: 0.0
Right: 0.13715553550041798

State: (3, 1)
Up: 4.825854511712306
Down: -0.03438123168566812
Left: 0.10867882029322147
Right: 1.0015572397722665

State: (3, 2)
Up: 5.875704328143301
Down: 0.9315770230698863
Left: 0.0006851481810742227
Right: 0.47794799892127526

State: (3, 3)
Up: 5.4028951599661275
Down: 2.6989177956329757
Left: -0.6454474033238188
Right: 0.018474082554518417